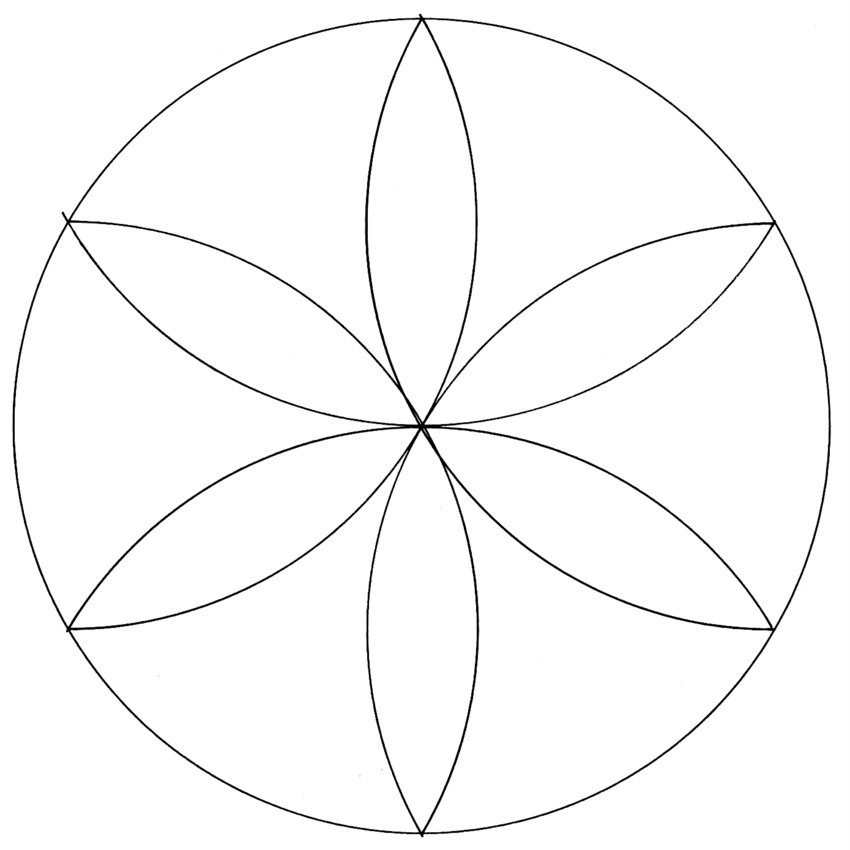
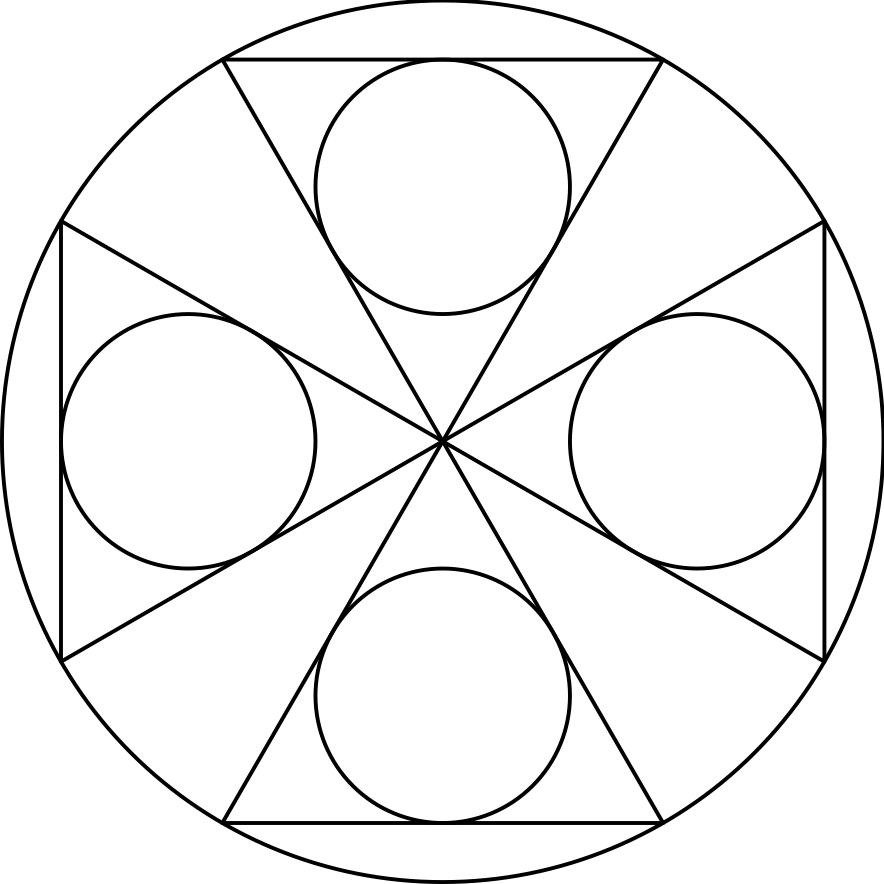
5. Case - Interface Design
Drawing with turtle
- The turtle module
- Simple repetition
- Encapsulation
- Generalization
- Interface design
- Refactoring
- docstring
This chapter presents a case study that demonstrates a process for designing functions that work together. It introduces the turtle module, which allows you to create images using turtle graphics.The turtle module is included in most Python installations.
https://docs.python.org/3/library/turtle.html
The turtle module
import turtle
leo = turtle.Turtle()
Create a file named my_polygon.py and type in the following code:
import turtle
leo = turtle.Turtle()
print(leo) #This tells us that leo refers to an object with type Turtle as defined in module turtle.
turtle.mainloop()
mainloop tells the window to wait for the user to do something, although in this case there’s not much for the user to do except close the window.
Then we call a method to move the small arrow around the window.
leo.fd(100)
Calling a method is like making a request: you are asking leo to move forward. The argument of fd is a distance in pixels, so the actual size depends on your display.
To draw a right angle, add these lines to the program (after creating leo and before calling mainloop):
leo.fd(100)
leo.lt(90)
leo.fd(100)
for i in range(4):
print('Hello!')
Exercise 02
The following sections have solutions to the exercises, so don’t look until you have finished (or at least tried).
1. Write a function called square that takes a parameter named t, which is a turtle. It should use the turtle to draw a square. Write a function call that passes leo as an argument to square, and then run the program again.
2. Add another parameter, named length, to square. Modify the body so length of the sides is length, and then modify the function call to provide a second argument. Run the program again. Test your program with a range of values for length.
3. Make a copy of square and change the name to polygon. Add another parameter named n and modify the body so it draws an n-sided regular polygon. Hint: The exterior angles of an n-sided regular polygon are 360/n degrees.
4. Write a function called circle that takes a turtle, t, and radius, r, as parameters and that draws an approximate circle by calling polygon with an appropriate length and number of sides. Test your function with a range of values of r.
Hint: figure out the circumference of the circle and make sure that length * n = circumference.
5. Make a more general version of circle called arc that takes an additional parameter angle, which determines what fraction of a circle to draw. angle is in units of degrees, so when angle=360, arc should draw a complete circle.
def square(t):
for i in range(4):
t.fd(100)
t.lt(90)
square(leo)
Inside the function, t refers to the same turtle leo, so t.lt(90) has the same effect as leo.lt(90). In that case, why not call the parameter leo? The idea is that t can be any turtle, not just leo, so you could create a second turtle and pass it as an argument to square:
raphael = turtle.Turtle()
square(raphael)
Wrapping a piece of code up in a function is called encapsulation.
def square(t, length):
for i in range(4):
t.fd(length)
t.lt(90)
square(leo, 100)
Adding a parameter to a function is called generalization because it makes the function more general: in the previous version, the square is always the same size; in this version it can be any size.
def polygon(t, n, length):
angle = 360 / n
for i in range(n):
t.fd(length)
t.lt(angle)
polygon(leo, 7, 70)
When a function has more than a few numeric arguments, it is easy to forget what they are, or what order they should be in. In that case it is often a good idea to include the names of the parameters in the argument list:
polygon(leo, n=7, length=70)
These are called keyword arguments because they include the parameter names as “keywords”. https://docs.python.org/3/tutorial/controlflow.html#keyword-arguments
This syntax makes the program more readable. It is also a reminder about how arguments and parameters work: when you call a function, the arguments are assigned to the parameters.
import math
def circle(t, r):
circumference = 2 * math.pi * r
n = 50
length = circumference / n
polygon(t, n, length)
The interface of a function is a summary of how it is used: what are the parameters? What does the function do? And what is the return value? An interface is “clean” if it allows the caller to do what they want without dealing with unnecessary details.
Rather than clutter up the interface, it is better to choose an appropriate value of n depending on circumference:
def circle(t, r):
circumference = 2 * math.pi * r
n = int(circumference / 3) + 1
length = circumference / n
polygon(t, n, length)
def arc(t, r, angle):
arc_length = 2 * math.pi * r * angle / 360
n = int(arc_length / 3) + 1
step_length = arc_length / n
step_angle = angle / n
for i in range(n):
t.fd(step_length)
t.lt(step_angle)
The second half of this function looks like polygon, but we can’t reuse polygon without changing the interface. We could generalize polygon to take an angle as a third argument, but then polygon would no longer be an appropriate name! Instead, let’s call the more general function polyline:
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
Now we can rewrite polygon and arc.
def polygon(t, n, length):
angle = 360.0 / n
polyline(t, n, length, angle)
def arc(t, r, angle):
arc_length = 2 * math.pi * r * angle / 360
n = int(arc_length / 3) + 1
step_length = arc_length / n
step_angle = float(angle) / n
polyline(t, n, step_length, step_angle)
Finally, we can rewrite circle:
def circle(t, r):
arc(t, r, 360)
This process - rearranging a program to improve interfaces and facilitate code reuse - is called refactoring. In this case, we noticed that there was similar code in arc and polygon, so we “factored it out” into polyline.
def polyline(t, n, length, angle):
"""Draws n line segments with the given length and
angle (in degrees) between them. t is a turtle.
"""
for i in range(n):
t.fd(length)
t.lt(angle)
Exercise 03
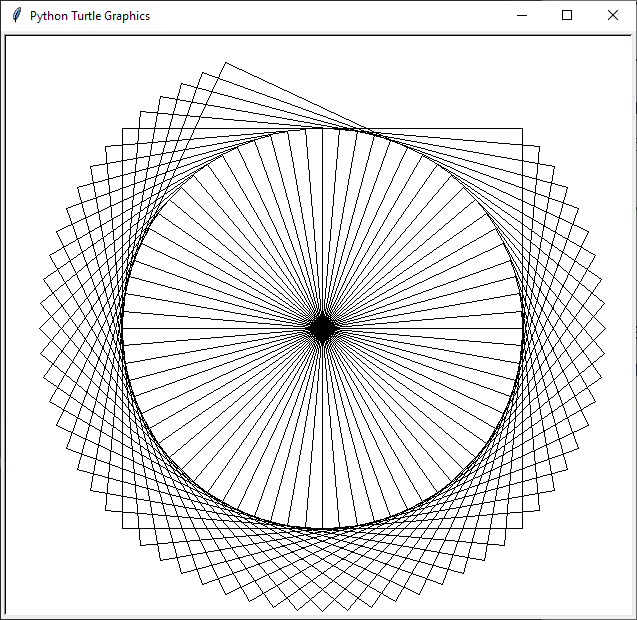
1. Write an appropriately general set of functions that can draw shapes as below. Tips: draw 60 squares, turning right 5 degrees after each square.
2. Write an appropriately general set of functions that can draw shapes as below. Tips: draw 60 squares, turning 5 degrees after each square and making each successive square bigger. Start at a length of 30 and increment 4 units every square.

3. Write an appropriately general set of functions that can draw shapes as below.
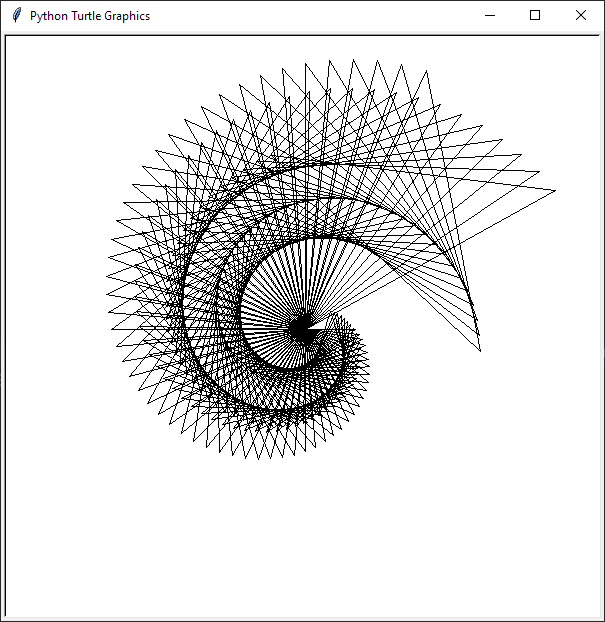
4. Write an appropriately general set of functions that can draw any other kind of spiral, such as an Archimedian spiral. Read more about spirals at http://en.wikipedia.org/wiki/Spiral.